Mechanics
Mechanics is the branch of physics that deals with the conditions of rest or motion of the material objects around us.
Sub-branches of Mechanics:
- Statics:
It deals with the study of objects at rest or in equilibrium, even when they are under the action of several forces. - Kinematics:
It deals with the study of the motion of objects without considering the cause of motion. - Dynamics:
It deals with the study of motion of objects taking into consideration the cause of their motion.
Rest and Motion
Also Check: Class 11 Physics thermo notes
Also Check: Class 11 Physics Vectors notes
Also check: Class 11 The Address Notes pdf
Rest:
An object is said to be at rest if it does not change its position with respect to its surroundings with the passage of time.
Example: A book lying on a table.
Motion:
An object is said to be in motion if it changes its position with respect to its surroundings with the passage of time.
Example: A train moving on rails.
Rest and Motion Are Relative
In order to know whether the position of an object changes with time or not, a point absolutely fixed in space has to be chosen as a reference point.
But no such point is known in the universe. The earth revolves around the sun, the entire solar system travels through our galaxy, the Milky Way, and clusters of galaxies move with respect to other clusters.
So, no object in the universe is in a state of absolute rest.
As no object in the universe is at absolute rest, so the absolute motion cannot be realised. Only the conditions of relative rest and relative motion can be realised.
Point Object
- If the position of an object changes by distances much greater than its own size in a reasonable duration of time, the object may be regarded as a point object.
- When a point object moves, its rotational and vibrational motions may be ignored.
Examples:
- Earth can be regarded as a point object for studying its motion around the sun.
- A train under a journey of several hundred kilometers can be regarded as a point object.
Motion in One, Two, and Three Dimensions

One-Dimensional Motion:
- The motion of an object is said to be one-dimensional if only one of the three coordinates specifying the position of the object changes with time.
- This motion is also called rectilinear or linear motion.
Examples:
- Motion of a train along a straight track.
- Motion of a freely falling body.
Two-Dimensional Motion:
- The motion of an object is said to be two-dimensional if only two of the three coordinates specifying its position change with time.
Examples:
- Motion of planets around the sun.
- A car moving in a zig-zag path on a level road.
Three-Dimensional Motion:
- The motion of an object is said to be three-dimensional if all three coordinates specifying its position change with time.
Examples:
- A kite flying on a windy day.
- Motion of an airplane in space.
Important Terms
Distance (or Path Length):
- It is the length of the actual path traversed by a body between its initial and final positions.
- Formula:
\( \text{Distance covered} = AC + CB \) - Key Points:
- Distance is a scalar quantity.
- Distance covered is always positive or zero.
- The SI unit of distance is metre (m).
Displacement:
- The displacement of an object is the change in the position of the object in a fixed direction.
- It is the shortest path measured in the direction from the initial point to the final point.
- Formula:
\( \text{Displacement} = \overrightarrow{AB} \)
Key Points:
- Displacement is a vector quantity.
- Displacement may be positive, negative, or zero.
- The SI unit of displacement is metre (m).
Speed
- The rate of change of position of an object with time in any direction is called its speed.
- Formula:
\[
\text{Speed} = \frac{\text{Distance travelled}}{\text{Time taken}}
\]
Key Points:
- Speed is a scalar quantity.
- Speed may be positive or zero but never negative.
- The SI unit of speed is m/s.
- Dimensional formula: \( [\text{Speed}] = [M^0 L^1 T^{-1}] \).
Different Types of Speed:
- Uniform Speed:
- An object is said to be moving with uniform speed if it covers equal distances in equal intervals of time, no matter how small these intervals may be.
- Variable Speed:
- An object is said to be moving with variable speed if it covers unequal distances in equal intervals of time.
Average Speed
- For an object moving with variable speed, the average speed is the total distance traveled by the object divided by the total time taken to cover that distance.
- Formula:
\[
\scriptsize \text{Average Speed} = \frac{\text{Total Distance Travelled}}{\text{Total Time Taken}}
\]
Instantaneous Speed
- The speed of an object at any particular instant of time or at a particular point of its path is called the instantaneous speed of the object.
- Formula:
\[
v = \lim_{\Delta t \to 0} \frac{\Delta x}{\Delta t} = \frac{dx}{dt}
\]
Here, \( \frac{dx}{dt} \) is the first-order derivative of distance ( x ) with respect to time ( t ). - Example: The speedometer of an automobile indicates its instantaneous speed at any instant.
Average Speed in Different Situations
1. A Body Covering Different Distances with Different Speeds
- Suppose a body covers distances \( s_1, s_2, s_3, \dots \) with speeds \( v_1, v_2, v_3, \dots \) respectively. The average speed is given by:
\[
v_{\text{avg}} = \frac{\text{Total Distance Travelled}}{\text{Total Time Taken}}
\]
\[
v_{\text{avg}} = \frac{s_1 + s_2 + s_3 + \dots}{t_1 + t_2 + t_3 + \dots}
\]
Using the relationship \( t = \frac{s}{v} \):
\[
v_{\text{avg}} = \frac{s_1 + s_2 + s_3 + \dots}{\left(\frac{s_1}{v_1} + \frac{s_2}{v_2} + \frac{s_3}{v_3} + \dots\right)}
\]
2. Special Case: If \( s_1 = s_2 = s \) (the body covers equal distances with different speeds):
\[
v_{\text{avg}} = \frac{2s}{\frac{s}{v_1} + \frac{s}{v_2}} = \frac{2v_1v_2}{v_1 + v_2}
\]
2. A Body Moving with Different Speeds in Different Time Intervals
- Suppose a body travels with speeds \( v_1, v_2, v_3, \dots \) in time intervals \( t_1, t_2, t_3, \dots \), the average speed is:
\[
v_{\text{avg}} = \frac{\text{Total Distance Travelled}}{\text{Total Time Taken}}
\]
Using \( s = v \cdot t \):
\[
v_{\text{avg}} = \frac{v_1t_1 + v_2t_2 + v_3t_3 + \dots}{t_1 + t_2 + t_3 + \dots}
\]
Special Case for Average Speed
- If \( t_1 = t_2 = t_3 = \dots = t_n = t \), then:
\[
v_{\text{avg}} = \frac{(v_1 + v_2 + v_3 + \dots + v_n) t}{nt}
\]
Simplified to:
\[
v_{\text{avg}} = \frac{v_1 + v_2 + v_3 + \dots + v_n}{n}
\]
Velocity
- The rate of change of position of an object with time in a given direction is called velocity.
- Formula:
\[
\text{Velocity} = \frac{\text{Displacement}}{\text{Time}}
\]
Key Points:
- Velocity is a vector quantity.
- Velocity can be positive, zero, or negative.
- The SI unit of velocity is m/s.
- Dimensional formula: \( [\text{Velocity}] = [M^0 L^1 T^{-1}] \).
Different Types of Velocities
- Uniform Velocity:
- A body is said to be moving with uniform velocity if it covers equal displacements in equal intervals of time, no matter how small these intervals may be.
- Variable Velocity:
- A body is said to be moving with variable velocity if either its speed changes, or its direction of motion changes, or both change with time.
- Average Velocity:
- For an object moving with variable velocity, average velocity is defined as the ratio of its total displacement to the total time interval in which that displacement occurs.
- Formula:
\[
\scriptsize \text{Average Velocity} = \frac{\text{Total Displacement}}{\text{Total Time}}
\] - If displacement is represented as \( x_2 – x_1 \) and time as \( t_2 – t_1 \):
\[
v_{\text{avg}} = \frac{x_2 – x_1}{t_2 – t_1} = \frac{\Delta x}{\Delta t}
\]
Instantaneous Velocity
- The velocity of an object at a particular instant of time or at a particular point of its path is called its instantaneous velocity.
- Formula:
\[
\vec{v} = \lim_{\Delta t \to 0} \frac{\Delta \vec{x}}{\Delta t} = \frac{d\vec{x}}{dt}
\]
Here, \( \frac{d\vec{x}}{dt} \) is the first-order derivative of displacement with respect to time.
Uniform Motion
- An object is said to be in uniform motion if it covers equal distances in equal intervals of time, no matter how small these intervals may be.
- The motion must be in the same fixed direction.
- Formula for distance travelled:
\[
s = v \cdot t
\]
Non-Uniform Motion
- A body is said to be in non-uniform motion if its velocity changes with time.
- This change may occur due to:
- A change in the speed of the body.
- A change in the direction of motion.
- Both speed and direction changing with time.
Acceleration
- The rate of change of velocity of an object with respect to time is called its acceleration.
- Formula:
\[
\text{Acceleration} = \frac{\text{Change in velocity}}{\text{Time taken}}
\]
Key Points:
- It is a vector quantity.
- SI unit is m/s².
- Dimensional formula: \( [\text{Acceleration}] = [M^0 L^1 T^{-2}] \).
Different Types of Acceleration
- Uniform Acceleration:
- The acceleration of an object is said to be uniform if its velocity changes by equal amounts in equal intervals of time, no matter how small the intervals may be.
- Variable Acceleration:
- The acceleration of an object is said to be variable if its velocity changes by unequal amounts in equal intervals of time.
- Average Acceleration:
- For an object moving with variable velocity, the average acceleration is defined as the ratio of the total change in velocity to the total time interval during which the change occurs.
- Formula:
\[
a_{\text{avg}} = \frac{v_2 – v_1}{t_2 – t_1} = \frac{\Delta v}{\Delta t}
\]
- Instantaneous Acceleration:
- The acceleration of an object at a particular instant of time or at a specific point in its motion is called instantaneous acceleration.
- Formula:
\[
a = \lim_{\Delta t \to 0} \frac{\Delta v}{\Delta t} = \frac{dv}{dt}
\] - If
- As \( v = \frac{dx}{dt} \), therefor we can write;
\[
a = \frac{d}{dt}\left(\frac{dx}{dt}\right) = \frac{d^2x}{dt^2}
\] - Instantaneous acceleration is the first-order derivative of velocity and the second-order derivative of displacement with respect to time.
Positive and Negative Acceleration
Positive Acceleration:
- If the velocity of an object increases with time, its acceleration is said to be positive.
- Example:
- When a bus leaves a bus stop, its acceleration is positive.
Negative Acceleration:
- If the velocity of an object decreases with time, its acceleration is said to be negative.
- Negative acceleration is also called retardation or deceleration.
- Example:
- When a bus slows down while approaching a bus stop, its acceleration is negative.
Kinematic Equations for Uniformly Accelerated Motion
- \( v = u + at \)
- \( s = ut + \frac{1}{2}at^2 \)
- \( v^2 = u^2 + 2as \)
- \( s_{nth} = u + \frac{a}{2}(2n-1) \)
Consider an object moving with constant acceleration along the positive direction of the X-axis:

- \( x_0 \): Position of the object at instant ( t = 0 )
- \( x \): Position of the object at instant ( t )
- \( u \): Velocity of the object at ( t = 0 )
- \( v \): Velocity of the object at instant ( t )
1. Velocity-Time Relation:
Acceleration:
\[
a = \frac{\text{Change in Velocity}}{\text{Time Taken}} = \frac{v – u}{t – 0}
\]
\[
\implies v – u = at
\]
\[
\implies v = u + at
\]
2. Distance-Time Relation:
The average velocity is equal to the total displacement covered divided by total time taken.
\[
\therefore v_{\text{avg}} = \frac{x – x_0}{t – 0} = \frac{x – x_0}{t}
\]
Also:
\[
v_{\text{avg}} = \frac{u + v}{2}
\]
Equating the two expressions for \( v_{\text{avg}} \):
\[
\frac{x – x_0}{t} = \frac{u + v}{2}
\]
\[
\implies x – x_0 = \left(\frac{u + v}{2}\right)t
\]
Substitute \( v = u + at \), we can write;
\[
x – x_0 = \left(\frac{u + (u + at)}{2}\right)t
\]
\[
\implies x – x_0 = \frac{2ut + at^2}{2}
\]
\[
\implies x – x_0 = ut + \frac{1}{2}at^2
\]
This equation is called the Position-Time Relation.
Let \( x – x_0 = s \) (distance traveled in time (t)), then we have;
\[
s = ut + \frac{1}{2}at^2
\]
3. Velocity-Distance Relation
We know that;
\[
v – u = at \tag{1}
\]
Also:
\[
x – x_0 = \frac{(v + u)}{2} \cdot t
\]
Using \( x – x_0 = s\), we can write;
\[
s = \frac{(v + u)}{2} \cdot t
\]
Rearranging it, we have; \[ {v+ u} = \frac {2s}{t} \tag{2} \]
Multiplying (1) and (2), we get
\[
(v – u)(v + u) = 2as
\]
\[
\implies v^2 – u^2 = 2as
\]
4. Distance Covered in the nth second
The distance traveled in the \( n^\text{th} \) second can be obtained by subtracting the distance traveled in the first \((n – 1) \) seconds from the distance traveled in the first ( n ) seconds.
Distance traveled in the first ( n ) seconds:
\[
s_n = ut + \frac{1}{2}an^2 \tag{1}
\]
Distance traveled in the first \( (n – 1) \) seconds:
\[
s_{n-1} = u(n – 1) + \frac{1}{2}a(n – 1)^2 \tag{2}
\]
Distance traveled in the \( n^\text{th} \) second is;
\[
s_{nth} = s_n – s_{n-1} \tag{3}
\]
Substitute the values of \(s_n – s_{n-1} \) from (1) and (2) into (3), we get;
\[
\scriptsize s_{nth} = un + \frac{1}{2}an^2 – \left[ u(n-1) + \frac{1}{2}a(n-1)^2 \right]
\]
Simplifying further, we can write;
\[
\scriptsize s_{nth} = un + \frac{1}{2}an^2 – un + u – \frac{1}{2}a(n^2 – 2n + 1)
\]
\[
\implies s_{nth} = u + an – \frac{1}{2}a
\]
\[
\implies s_{nth} = u + a\left(n – \frac{1}{2}\right)
\]
\[
\implies s_{nth} = u + \frac{a}{2}(2n – 1)
\]
Motion Under Gravity | Free Fall
- In the absence of air resistance, all bodies fall with the same acceleration near the surface of the earth.
- This motion of a body falling toward the earth from a small height is called free fall.
- The acceleration with which a body falls is called acceleration due to gravity and is denoted by g.
Value near the surface of the earth:
\[
g = 9.8 \, \text{m/s}^2
\]
Equations of Motion for a Freely Falling Body
- \( v = u + gt \)
- \( s = ut + \frac{1}{2}gt^2 \)
- \( v^2 – u^2 = 2gs \)
Note:
- When a body falls freely under the action of gravity, its velocity increases and the value of ( g ) is taken as positive.
- When a body is thrown vertically upward, its velocity decreases and the value of ( g ) is taken as negative.
Position-Time Graphs (x-t graphs)
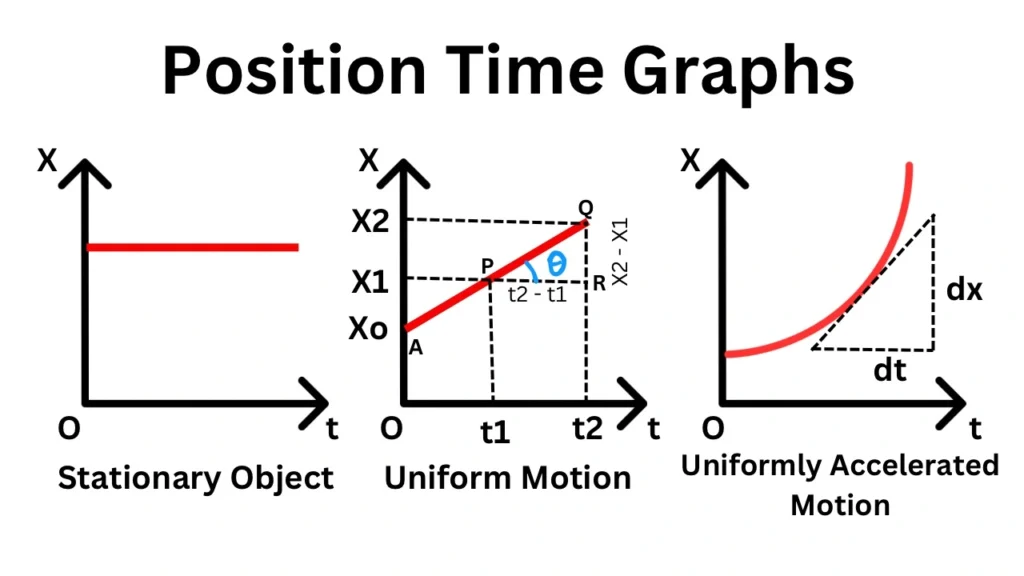
1. Position-Time Graph for a Stationary Object:
- The graph remains a straight horizontal line as the position does not change over time.
2. Position-Time Graph for Uniform Motion:
- The position-time graph for an object in uniform motion along a straight-line path is a straight line inclined to the time-axis.
Slope of \( x \)-\( t \) graph AB:
\[
\text{slope} = \tan \theta = \frac{\text{QR}}{\text{PR}} = \frac{x_2 – x_1}{t_2 – t_1}
\]
\[
\text{slope} = \frac{\text{Displacement}}{\text{Time}} = \text{Velocity}.
\]
- Conclusion:
The slope of the position-time graph gives the velocity of the object.
3. Position-Time Graph for Uniformly Accelerated Motion:
- The position-time relation for uniformly accelerated motion along a straight line is:
\[
x = x_0 + ut + \frac{1}{2}at^2
\]
Clearly, \( x \propto t^2 \).
Thus, the position-time graph for uniformly accelerated motion is a parabola.
Note:
\[
\text{slope} = \frac{dx}{dt} = \text{Velocity}.
\]
Velocity-Time (v -t) Graphs

1. Velocity-Time Graph for Uniform Motion:
- The velocity-time graph for uniform motion is a straight line parallel to the time-axis.
Area under the ( v )-( t ) graph between time \( t_1 \) and \( t_2 \):
\[
\text{Area} = \text{Area of rectangle ABCD}
\]
\[
\implies \text{Area} = \text{AD} \times \text{DC}
\]
\[
\implies \text{Area} = v \times (t_2 – t_1)
\]
\[
\implies \text{Area} = \text{velocity} \times \text{time}
\]
\[
\implies \text{Area} = \text{Displacement.}
\]
Conclusion:
The area under the ( v )-( t ) graph gives the displacement of the object in the given time interval.
2. Velocity-Time Graph for Uniformly Accelerated Motion:
- The velocity-time graph for uniformly accelerated motion is a straight line inclined to the time-axis.
Slope of the ( v )-( t ) graph:
\[
\scriptsize \text{slope} = \frac{\text{BC}}{\text{AC}} = \frac{\text{Change in velocity}}{\text{Time}} = \text{Acceleration}.
\]
Conclusion:
The slope of the velocity-time graph gives the acceleration of the object.
Area under the ( v )-( t ) graph:
\[
\scriptsize \text{Area} = \text{Area of trapezium OABCD} = \frac{1}{2} \left[\text{OA} + \text{BD}\right] \times \text{OD}
\]
\[
= \frac{1}{2} (u + v) \times t
\]
\[= \text{Average velocity} \times \text{time}. \]
Conclusion:
The area under the velocity-time graph gives the distance traveled by the object in the given time interval.
Derivation of Equations of Motion by Graphical Method
Consider an object moving along a straight-line path with initial velocity \( u \) and uniform acceleration \( a \).
Suppose it travels a distance \( s \) in time \( t \).

(i) Velocity-Time Relation:
From the \( v \)-\( t \) graph:
\[
\text{Acceleration} = \text{slope of } v \text{-} t \text{ graph}
\]
\[
\implies a = \frac{\text{BC}}{\text{AC}} = \frac{v – u}{t}
\]
\[
\implies v – u = at
\]
\[
\implies v = u + at
\]
This is the first equation of motion.
(ii) Distance-Time Relation:
The distance traveled is equal to the area under the \( v \)-\( t \) graph:
\[
\scriptsize \text{Distance traveled} = \text{Area of trapezium OABD}
\]
\[
\scriptsize s = \text{Area of rectangle OACD} + \text{Area of triangle ABC}
\]
\[
\implies s = (\text{OA} \times \text{OD}) + \frac{1}{2} (\text{BC} \times \text{AC})
\]
\[
\implies s = ut + \frac{1}{2} (v – u) \times t
\]
\[
\implies s = ut + \frac{1}{2} at \times t
\]
\[
\implies s = ut + \frac{1}{2} at^2
\]
This is the second equation of motion.
(iii) Velocity-Displacement Relation:
Distance traveled is given by \( s = \text{Area of trapezium OABD} \)
\[
\implies s = \frac{1}{2} (\text{OA} + \text{BD}) \times \text{OD}
\]
\[
\implies s = \frac{1}{2} (u + v) \times t
\]
Substituting \( t = \frac{v – u}{a} \), we get;
\[
s = \frac{1}{2} (u + v) \times \frac{v – u}{a}
\]
\[
\implies (v + u)(v – u) = 2as
\]
\[ \implies v^2 – u^2 = 2as \]
This is the third equation of motion.
Distance Time Graphs
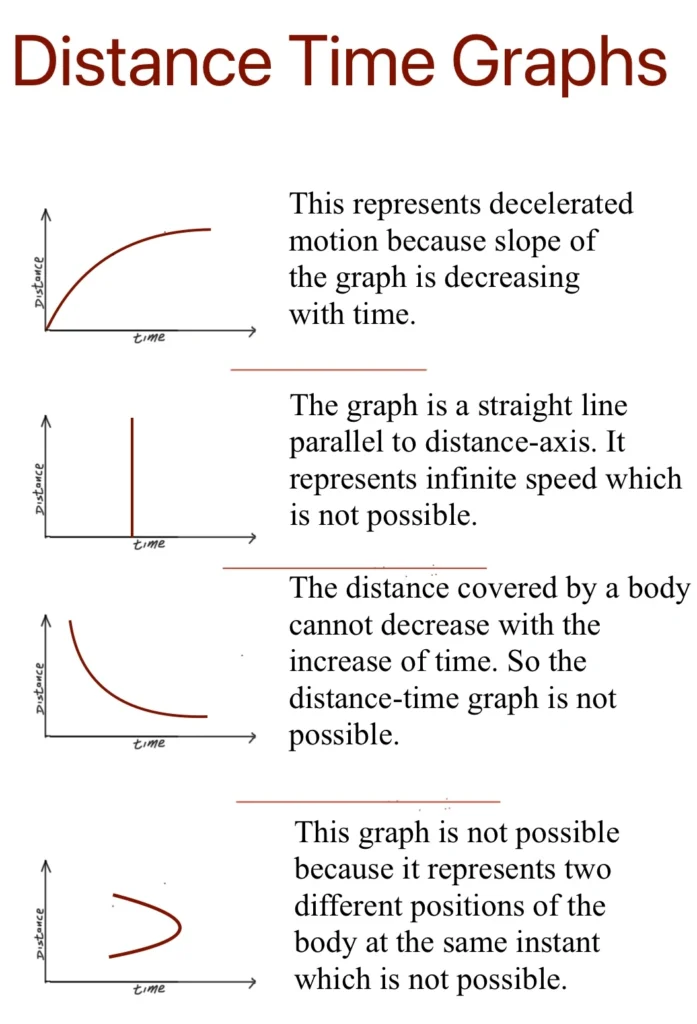
Relative Velocity
- The relative velocity of an object ( 2 ) with respect to object ( 1 ), when both are in motion, is the time rate of change of position of object ( 2 ) with respect to that of object ( 1 ).
(1) Relative Velocity of object 2 with respect to object 1 is given by;
\[
\vec{v_{21}} = \vec{v_2} – \vec{v_1}
\]
(2) Similarly Relative Velocity of object 2 with respect to object 1 is given by;
\[
\vec{v_{12}} = \vec{v_1} – \vec{v_2}
\]
Determination of Relative Velocity
- The relative velocity of a body ( A ) with respect to another body ( B ), when both are in motion, can be obtained by adding to the velocity of ( A ), a velocity equal and opposite to that of ( B ):
\[
v_{AB} = v_A + (-v_B)
\] - This law can also be applied to bodies moving in directions inclined to each other.
Case: Two Bodies Moving at an Angle
- Consider two bodies ( A ) and ( B ) moving with velocities \( v_A \) and \( v_B \), respectively, making an angle \( \theta \) with each other.
- To find the relative velocity \( v_{AB} \) of ( A ) with respect to ( B ), we add \( v_A \) and \( -v_B \) as vectors.
Relative Velocity Magnitude:
\[
v_{AB} = \sqrt{v_A^2 + v_B^2 + 2v_Av_B \cos(180^\circ – \theta)}
\]
\[
v_{AB} = \sqrt{v_A^2 + v_B^2 – 2v_Av_B \cos \theta}
\]
Suppose the relative velocity \( \vec{V_{AB}} \) makes angle \( \beta \) with \( \vec{V}_A \).
Then
\[
\tan \beta = \frac{V_B \sin \theta}{V_A – V_B \cos \theta}
\]
or
\[
\beta = \tan^{-1} \left( \frac{V_B \sin \theta}{V_A – V_B \cos \theta} \right)
\]
Special case:
- When both the bodies are moving along parallel straight lines in the same direction. \(\theta = 0^\circ \)
\[
V_{AB} = \sqrt{V_A^2 + V_B^2 + 2V_A V_B \cos (180^\circ – 0^\circ)}
\]
\[
V_{AB} = \sqrt{V_A^2 + V_B^2 – 2V_A V_B}
\]
\[
V_{AB} = \sqrt{(V_A – V_B)^2} = V_A – V_B
\] - When the two bodies are moving along parallel straight lines in opposite directions. \(\theta = 180^\circ \)
\[
V_{AB} = \sqrt{V_A^2 + V_B^2 + 2V_A V_B \cos 180^\circ}
\]
\[
V_{AB} = \sqrt{V_A^2 + V_B^2 – 2V_A V_B \cos 180^\circ}
\]
\[
V_{AB} = \sqrt{(V_A + V_B)^2}
\]
\[
V_{AB} = V_A + V_B
\]
Thus, the relative velocity of body ( A ) w.r.t. body ( B ) is equal to the sum of the magnitudes of their velocities. That is why, when two fast trains cross each other in opposite directions, each appears to go very fast relative to the other.