Wave or Wave Motion
A wave motion is a kind of disturbance which travels through a medium due to repeated vibration of the particles of the medium about their mean positions, the disturbance being handed over from one particle to the next.
Types of Waves
a) Mechanical Waves
The waves which require a material medium for their propagation are called mechanical waves. Such waves are also called elastic waves.
Examples: Water waves, sound waves, seismic waves, etc.
b) Electromagnetic Waves
The waves which travel in the form of oscillating electric and magnetic fields are called electromagnetic waves. Such waves do not require any material medium for their propagation and are also called non-mechanical waves.
Examples: Visible light, ultraviolet, infrared, radio waves, microwaves, X-rays, etc.
c) Matter Waves
The waves associated with microscopic particles such as electrons, protons, neutrons, atoms, molecules, etc., when they are in motion, are called matter waves or de-Broglie waves.
On the basis of oscillation with respect to the direction of propagation, waves can also be divided into the following two categories;
Transverse Waves: These are the waves in which the individual particles of the medium oscillate perpendicular to the direction of wave propagation.
Points of maximum displacement in the upward direction are called crests (denoted by c).
Points of maximum displacement in the downward direction are called troughs (denoted by T).

Longitudinal Waves: These are the waves in which the individual particles of the medium oscillate along the direction of wave propagation.
The waves travel in the form of alternate compressions (C) and rarefactions (R).
Example: Sound waves produced in air are longitudinal waves.
Definitions Related to Wave Motion
a) Amplitude (A): It is the maximum displacement suffered by the particles of the medium about their mean positions.
b. Time Period (T): It is the time in which a particle of the medium completes one vibration to and fro about its mean position.
c. Frequency (ν): The frequency of a wave is the number of waves produced per unit time in the given medium.
It is equal to the reciprocal of the time period:
\[
\nu = \frac{1}{T}
\]
SI Unit: \( \nu \) is measured in \( \text{s}^{-1} \) or Hertz (Hz).
d. Angular Frequency (ω): The rate of change of phase with time is called angular frequency of the wave.
\[
\omega = \frac{2\pi}{T} = 2\pi \nu
\]
SI Unit: \( \omega \) is measured in \( \text{rad/s} \).
e. Wavelength (λ): It is the distance covered by a wave during its time period. Or, it is the distance between two nearest particles of the medium which are vibrating in the same phase.
f. Wave Number (ν̅): The number of waves present in a unit distance of the medium is called wave number.
\[
\bar{\nu} = \frac{1}{\lambda}
\]
SI Unit: \( \bar{\nu} \) is measured in \( \text{m}^{-1} \).
g. Angular Wave Number or Propagation Constant (k): The quantity \( \frac{2\pi}{\lambda} \) is called angular wave number.
\[
k = \frac{2\pi}{\lambda}
\]
SI Unit: \( k \) is measured in \( \text{rad/m} \).
h. Wave Velocity or Phase Velocity (v): The distance covered by a wave per unit time in its direction of propagation is called wave velocity.
Also Check: Class 11 English The Address Notes
Also Check: Class 11 English The Ailing Planet Notes
Relation Between Wave Velocity, Frequency, and Wavelength
Wave velocity = Distance / Time
\[
v = \frac{\lambda}{T} = \lambda \nu
\]
Speed of Transverse Waves
a) Speed of a Transverse Wave on a Stretched String
\[
v = \sqrt{\frac{T}{m}}
\]
Where:
- \( T \): Tension in the string
- \( m \): Mass per unit length or linear mass density
Note: The speed does not depend on the frequency of the wave.
b) Speed of a Transverse Wave in a Solid
\[
v = \sqrt{\frac{\eta}{\rho}}
\]
Where:
- \( \eta \): Elasticity of shape or modulus of rigidity of the solid
- \( \rho \): Density
Example: A steel wire 0.72 m long has a mass of \( 5 \times 10^{-3} \, \text{kg} \). If the wire is under a tension of 60 N, what is the speed of transverse waves on the wire?
Solution:
\[
v = \sqrt{\frac{T}{m}} \tag{1}
\]
\[
T = 60 \, \text{N}, \\ \quad m = \frac{5 \times 10^{-3}}{0.72} = 6.9 \times 10^{-3} \, \text{kg/m}
\]
Using these values in (1), we cab write
\[
v = \sqrt{\frac{60}{6.9 \times 10^{-3}}} \approx 93 \, \text{ms}^{-1}
\]
Speed of a Longitudinal Wave
Speed of a Longitudinal Wave in a Liquid or Gas
\[
v = \sqrt{\frac{B}{\rho}}
\]
Where:
- \( B \): Bulk modulus or volume elasticity
- \( \rho \): Density of the fluid
Speed of a Longitudinal Wave in a Solid Rod
\[
v = \sqrt{\frac{Y}{\rho}}
\]
Where:
- \( Y \): Young’s modulus
- \( \rho \): Density
Progressive Wave
A wave that travels from one point of the medium to another is called a progressive wave.
A progressive wave may be transverse or longitudinal.
Plane Progressive Harmonic Wave
If, during the propagation of a wave through a medium, the particles of the medium vibrate simple harmonically about their mean position, then the wave is said to be a plane progressive harmonic wave.
Displacement Relation for a Progressive Harmonic Wave
The displacement of the particle at the origin \((x = 0) \) at any instant (t) is given by:
\[
y(0, t) = A \sin \omega t \tag{1}
\]
Where: \(A \) = Amplitude
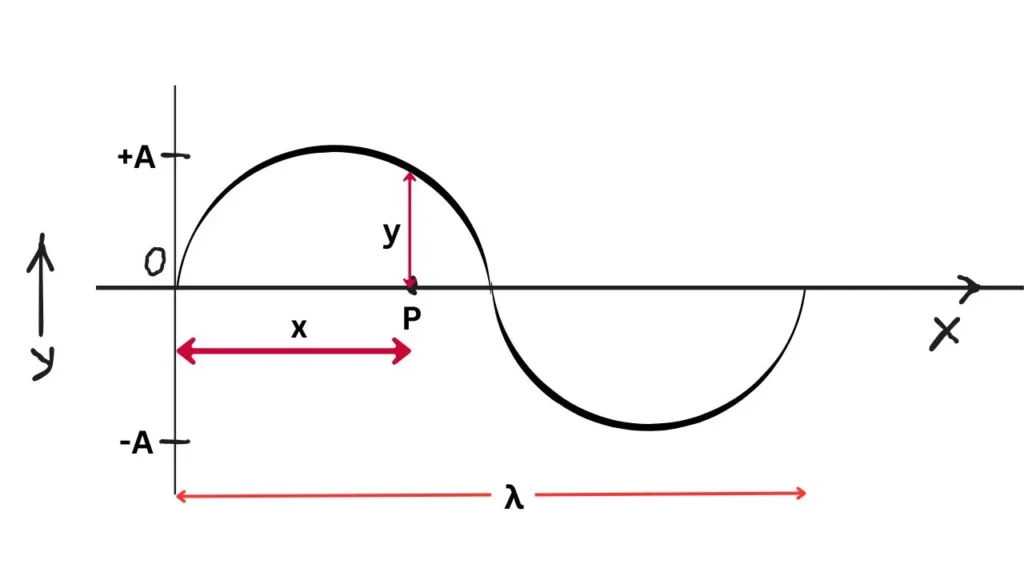
Consider a particle “P” on the X-axis at a distance (x) from the origin.
The disturbance traveling from the origin (O) will reach (P) in \(\frac{x}{v} \) seconds, where (v) is the wave velocity.
This means the particle “P” will start vibrating \(\frac{x}{v} \) seconds later than the particle at (O).
Thus, the displacement of the particle at (P) at any instant (t) is equal to the displacement of the particle at O at a time \( \frac{x}{v} \) seconds earlier.
It can be written as:
\[
y(x, t) = A \sin \omega \left(t – \frac{x}{v}\right)
\]
Substitute \(\omega = \frac{2\pi}{T} \) and \(v = \frac{\lambda}{T} \), we get:
\[
y(x, t) = A \sin (\omega t – kx)
\]
Where \(k = \frac{2\pi}{\lambda} \) is the propagation constant (wave number).
This equation represents a harmonic wave traveling along the positive direction of the X-axis.
It can also be written in the following forms:
\[
y(x, t) = A \sin \left( \frac{2\pi}{T}t – \frac{2\pi}{\lambda}x \right)
\]
or
\[
y(x, t) = A \sin 2\pi \left( \frac{t}{T} – \frac{x}{\lambda} \right)
\]
Including Initial Phase
If the initial phase of the particle at (O) is \(\phi_0 \), then the equation of wave motion becomes:
\[
y(x, t) = A \sin (\omega t – kx + \phi_0)
\]
Where:
- Displacement: \(y(x, t) \)
- Amplitude: \(A \)
- Phase: \((\omega t – kx + \phi_0) \)
- Angular Frequency: \(\omega \)
- Wave Number: \(k \)
- Initial Phase: \(\phi_0 \)
Harmonic Wave Traveling in the Negative X-Direction
The equation for a harmonic wave traveling along the negative X-axis is:
\[
y(x, t) = A \sin (\omega t + kx + \phi_0)
\]
Phase of a Wave
The phase of a harmonic wave is a quantity that gives complete information of the wave at any time and at any position.
Particle Velocity (V)
It is the velocity with which the particles of the medium vibrate about their mean positions.
\[
V = \frac{dy}{dt} = \omega A \cos(\omega t – kx)
\]
The maximum particle velocity or the velocity amplitude is:
\[
V_0 = \omega A = \frac{2\pi A}{T}
\]
Particle Acceleration (a)
The acceleration of the particle is given by:
\[
a = \frac{dV}{dt} = -\omega^2 A \sin(\omega t – kx)
\]
\[
a = -\omega^2 y
\]
The maximum value of particle acceleration or the acceleration amplitude is:
\[
a_0 = \omega^2 A
\]
Wave Velocity or Phase Velocity \((v) \)
The distance covered by a wave in the direction of its propagation per unit time is called the wave velocity.
\[
v = \frac{\lambda}{T} = \lambda \nu
\]
Reflection of waves and boundary effects
Reflection of a Wave from a Rigid Boundary: When a traveling wave is reflected from a rigid boundary, it is reflected back with a phase reversal or a phase difference of \(\pi \) radians.
Reflection of a Wave from an Open Boundary: When a traveling wave is reflected from a free or open boundary, it suffers no phase change.
Suppose an incident wave is represented by:
\[
y_i(x, t) = A \sin (\omega t – kx)
\]
For reflection at a rigid boundary, the reflected wave can be represented as:
\[
y_r(x, t) = -A \sin (\omega t + kx)
\]
For reflection at an open boundary, the reflected wave can be represented as:
\[
y_r(x, t) = A \sin (\omega t + kx)
\]
Principle of Superposition of Waves
The principle of superposition of waves states that when a number of waves travel through a medium simultaneously, the resultant displacement of any particle of the medium at any given time is equal to the algebraic sum of the displacements due to the individual waves.
\[
y = y_1 + y_2 + y_3 + \dots + y_n
\]
Stationary Waves
When two identical waves of the same amplitude and frequency traveling in opposite directions with the same speed along the same path superpose on each other, the resultant wave does not travel in either direction and is called a stationary or standing wave.
- Some particles of the medium remain permanently at rest. That is they have zero displacement. These positions are called nodes.
- Some other particles always suffer maximum displacement. These positions are called antinodes.
Necessary condition for the formation of stationary waves
A stationary wave cannot be formed from two independent waves travelling in a medium in opposite directions. In actual practice, a stationary wave is produced when a progressive wave and its reflected wave are superposed. Hence, a stationary wave can be produced only in a finite medium which has its boundaries.
Two types of stationary waves
a) Transverse stationary waves: When 2 identical transverse waves travelling in opposite directions overlap, a transverse stationary wave is formed.
b) Longitudinal stationary waves: When 2 identical longitudinal waves travelling in opposite directions overlap, a longitudinal stationary wave is formed.
Analytical treatment of stationary waves
Consider two sinusoidal waves of equal amplitude and frequency travelling along a long string in opposite directions.
The wave travelling along the positive \( x \)-direction can be represented as:
\[
y_1 = A \sin (\omega t – kx)
\]
The wave travelling along the negative \( x \)-direction can be represented as:
\[
y_2 = A \sin (\omega t + kx)
\]
The resultant wave is given by:
\[
y = y_1 + y_2
\]
Substituting the values:
\[
y = A \sin (\omega t – kx) + A \sin (\omega t + kx)
\]
Using the trigonometric identity:
\[
\sin a + \sin b = 2 \sin \left(\frac{a + b}{2}\right) \cos \left(\frac{a – b}{2}\right)
\]
We get:
\[
y = 2A \sin (\omega t) \cos (kx)
\]
Thus, the equation of the stationary wave becomes:
\[
y = (2A \cos kx) \sin \omega t
\]
This equation represents a stationary wave.
Clearly, the stationary wave has the same frequency \( \omega \) but has an amplitude equal to \( 2A \cos kx \).
Amplitude varies harmonically with the location \( x \) of the particle.
The amplitude will be zero at points where:
\[
\cos kx = 0
\]
or
\[
kx = \left(n + \frac{1}{2}\right)\pi
\]
where \( n = 0, 1, 2, 3, \ldots \).
Rewriting:
\[
\frac{2\pi}{\lambda}x = \left(n + \frac{1}{2}\right)\pi
\]
\[
x = \frac{(2n+1)\lambda}{4}
\]
Thus:
\[
x = \frac{\lambda}{4}, \frac{3\lambda}{4}, \frac{5\lambda}{4}, \ldots
\]
These positions of zero amplitude are called nodes. Clearly, the separation between two consecutive nodes is:
\[
\frac{\lambda}{2}
\]
The amplitude will have a maximum value of ( 2A ) at points where:
\[
\cos kx = \pm 1
\]
or
\[
kx = n\pi \quad \text{where } n = 0, 1, 2, 3, \ldots
\]
Rewriting:
\[
\frac{2\pi}{\lambda}x = n\pi
\]
\[
x = n\frac{\lambda}{2}
\]
Thus:
\[
x = 0, \frac{\lambda}{2}, \frac{3\lambda}{2}, \ldots
\]
These positions of maximum amplitude are called antinodes.
Comparison between stationary and progressive waves
| Progressive Waves | Stationary Waves |
|---|---|
| 1. The disturbance travels forward with a definite velocity. | 1. The disturbance remains confined to the region where it is produced. |
| 2. Each particle of the medium executes SHM about its mean position with the same amplitude. | 2. Except at nodes, all particles of the medium execute SHM with varying amplitude. |
| 3. There is a continuous change of phase from one particle to the next. | 3. All the positions between two successive nodes vibrate in the same phase, but the phase reverses for particles in the next pair of nodes. |
| 4. No particle of the medium is permanently at rest. | 4. The particles of the medium at nodes are permanently at rest. |
| 5. There is no instant when all the particles are at their mean positions together. | 5. Twice during each cycle, all particles pass through their mean positions simultaneously. |
| 6. There is a flow of energy across every plane along the direction of propagation of the wave. | 6. Energy of one region remains confined in that region. |
Normal Modes of Vibration of a Stretched String
Consider a string of length \( L \) clamped to rigid supports at its ends. If the string is plucked in the middle, transverse waves travel along it and get reflected from the ends. These identical waves traveling in opposite directions give rise to stationary waves.
If this string is stretched under tension \( T \). Let \( m \) be the mass per unit length of the string. The speed of the transverse wave on the string will be:
\[
v = \sqrt{\frac{T}{m}}
\]
As the two ends of the string are fixed, they remain at rest. So, there is a node \( N \) at each end.
First Mode of Vibration
If the string is plucked in the middle and released, it vibrates in one segment with nodes at its ends and an antinode in the middle.
Here, length of the string:
\[
L = \frac{\lambda_1}{2}
\]
or
\[
\lambda_1 = 2L
\]
Frequency of vibration:
\[
\nu_1 = \frac{v}{\lambda_1} = \frac{1}{2L} \sqrt{\frac{T}{m}}
\]
This is the minimum frequency with which the string can vibrate and is called the fundamental note or first harmonic.
Second mode of vibration
If the string is pressed in the middle and plucked at one-fourth length, then the string vibrates in two segments.
Here \( L = \frac{\lambda_2}{2} \)
or \( \lambda_2 = 2L \)
Therefore, the frequency of vibration,
\[
\nu_2 = \frac{v}{\lambda_2} = \frac{1}{L} \sqrt{\frac{T}{m}} = 2\nu
\]
This frequency is called the first overtone or second harmonic.
Third mode of vibration
If the string is pressed at one-third of its length from one end and plucked at one-sixth length, it will vibrate in three segments.
Then \( L = \frac{3 \lambda_3}{2} \) or \( \lambda_3 = \frac{2L}{3} \)
Therefore, the frequency of vibration,
\[
\nu_3 = \frac{v}{\lambda_3} = \frac{3}{2L} \sqrt{\frac{T}{m}} = 3\nu
\]
This frequency is called the second overtone or third harmonic.
In general,
\[
\nu_p = \frac{p}{2L} \sqrt{\frac{T}{m}} = p\nu
\]
where \( p \) → no. of segments.
Organ pipe
It is the simplest musical instrument in which sound is produced by setting an air column into vibrations.
- If both the ends of the pipe are open, it is called an open pipe.
- If one end of the pipe is closed, it is called a closed pipe.
Normal modes of vibration of an open organ pipe
1. First mode of vibration
There is one node in the middle and two antinodes at the ends of the pipe.
Here, the length of the pipe,
\[
L = 2 \cdot \frac{\lambda_1}{4} = \frac{\lambda_1}{2}
\]
or
\[
\lambda_1 = 2L
\]
Frequency of vibration,
\[
\nu_1 = \frac{v}{\lambda_1} = \frac{1}{2L} \sqrt{\frac{P}{S}} = \nu
\]
This frequency is called the fundamental frequency or first harmonic.
2. Second mode of vibration
Here, antinodes at the open ends are separated by two nodes and one antinode.
\[
L = 2 \cdot \frac{\lambda_2}{4} = \lambda_2
\]
or
\[
\lambda_2 = L
\]
Frequency,
\[
\nu_2 = \frac{v}{\lambda_2} = \frac{1}{L} \sqrt{\frac{P}{S}} = 2\nu
\]
This frequency is called the first overtone or second harmonic.
3. Third mode of vibration
Here, the antinodes at the open ends are separated by 3 nodes and 2 antinodes.
\[
L = 6 \cdot \frac{\lambda_3}{4}
\]
or
\[
\lambda_3 = \frac{2L}{3}
\]
Therefore,
\[
\nu_3 = \frac{v}{\lambda_3} = \frac{3}{2L} \sqrt{\frac{P}{S}} = 3\nu
\]
This frequency is called the second overtone or third harmonic.
Hence, various frequencies of an open organ pipe are in the ratio \(1 : 2 : 3 : 4 : \cdots \). These are called harmonics.
Normal modes of vibration of a closed organ pipe
1. First mode of vibration
There is only one node at the closed end and one antinode at the open end.
If \( L \) is the length of the organ pipe,
\[
L = \frac{\lambda_1}{4}
\]
or
\[
\lambda_1 = 4L
\]
Frequency,
\[
\nu_1 = \frac{v}{\lambda_1} = \frac{1}{4L} \sqrt{\frac{P}{S}} = \nu
\]
This frequency is called the first harmonic or fundamental frequency.
2. Second mode of vibration
There is one node and one antinode between a node at the closed end and an antinode at the open end.
\[ L = \frac{3\lambda_2}{4} \]
or
\[ \lambda_2 = \frac{4L}{3} \]
Frequency,
\[ v_2 = \frac{v}{\lambda_2} = \frac{3v}{4L} \sqrt{\frac{P}{\rho}} = \frac{3v}{4L} \]
This frequency is called first overtone or third harmonic.
3. Third mode of vibration
There are two nodes and two antinodes between a node at the closed end and an antinode at the open end.
\[ L = \frac{5\lambda_3}{4} \]
or
\[ \lambda_3 = \frac{4L}{5} \]
Frequency,
\[ v_3 = \frac{v}{\lambda_3} = \frac{5v}{4L} \sqrt{\frac{P}{\rho}} = \frac{5v}{4L} \]
This frequency is called second overtone or fifth harmonic.
Hence, different frequencies produced in a closed organ pipe are in the ratio 1:3:5:7…, i.e., only odd harmonics are present in a closed organ pipe.
Question: A pipe 30 cm long is open at both ends. Which harmonic mode of the pipe is resonantly excited by a 1.1 kHz source? Will resonance with the same source be observed if one end of the pipe is closed? Take the speed of sound in air as \( 330 \, \text{m/s} \).
Solution:
Fundamental frequency of the open pipe,
\[ v_1 = \frac{v}{2L} = \frac{330}{2 \times 0.3} = 550 \, \text{Hz} \]
Second harmonic,
\[ v_2 = 2v_1 = 2 \times 550 = 1100 \, \text{Hz} \]
Third harmonic,
\[ v_3 = 3v_1 = 3 \times 550 = 1650 \, \text{Hz} \]
and so on…
Clearly, a source of frequency \( 1100 \, \text{Hz} \, (1.1 \, \text{kHz}) \) will resonantly excite the second harmonic of the open pipe.
If one end of the pipe is closed, its fundamental frequency becomes:
\[
v_1 = \frac{v}{4L} = \frac{330}{4 \times 0.30} = 275 \, \text{Hz}
\]
Only odd harmonics are present in a closed pipe.
Third harmonic,
\[
v_3 = 3v_1 = 3 \times 275 = 825 \, \text{Hz}
\]
Fifth harmonic,
\[
v_5 = 5v_1 = 5 \times 275 = 1375 \, \text{Hz}
\]
and so on…
As no frequency of the closed pipe matches with the source frequency \( 1.1 \, \text{kHz} \), no resonance will be observed with the source.
Beats
The periodic variations in the intensity of sound caused by the superposition of two sound waves of slightly different frequencies are called beats.
Beat frequency is equal to the difference in frequencies of the two superposing waves.
Also Check: Thermodynamics class 11 Physics notes pdf